सामान्यीकृत झूठ सिद्धांत और अनुप्रयोगों का जर्नल

We briefly describe recent results about higher Bruhat and Tamari orders, the associated simplex equations and generalizations (polygon equations) of the pentagon equation, and the appearance of these orders in soliton interactions.

We provide a recursive classification of meander graphs, showing that each meander is identified by a unique sequence of fundamental graph theoretic moves. This sequence is called the meander’s signature and can be used to construct arbitrarily large sets of meanders, Frobenius or otherwise, of any size and configuration. In certain special cases, the signature is used to produce an explicit formula for the index of seaweed Lie subalgebra of sl(n) in terms of elementary functions.

In this paper, we introduce generalized left-Hom-symmetric algebras and generalized Hom-dendriform algebras as well as the corresponding modules. We investigate the connection between these categories of generalized Homalgebras and modules. We give various constructions of these generalized Hom-algebra structures from either a given one or an ordinary one. We prove that any generalized Hom-dialgebras give rise to generalized Hom-Leibniz- Poisson algebras and generalized Hom-Poisson dialgebras.

We present an Euler-Poincar´e (EP) formulation of a new class of peakon equations with cubic nonlinearity, viz., Fokas-Qiao and V. Novikov equations, in two almost equivalent ways. The first method is connected to flows on the spaces of Hill’s and first order differential operator and the second method depends heavily on the flows on space of tensor densities. We give a comparative analysis of these two methods. We show that the Hamiltonian structures obtained by Qiao and Hone and Wang can be reproduced by EP formulation. We outline the construction for the 2+1-dimensional generalization of the peakon equations with cubic nonlinearity using the action of the loop extension of Vect(S¹) on the space of tensor densities.

The present paper is about the problem of the passage to the limit from finite truncated systems to infinite system of linear algebraic equations. We consider the four important relations that arise in dealing with finite truncated Gaussian systems. These remarkable relations in fact give the opportunity to make transition from the solutions of finite systems to the solution of infinite system.

The author reviews his results on locally compact homogeneous spaces with inner metric, in particular, homogeneous manifolds with inner metric. The latter are isometric to homogeneous (sub-) Finslerian manifolds; under some additional conditions they are isometric to homogeneous (sub)-Riemannian manifolds. The class Ω of all locally compact homogeneous spaces with inner metric is supplied with some metric d_BGH such that 1) (Ω, d_BGH) is a complete metric space; 2) a sequences in (Ω, d_BGH) is converging if and only if it is converging in Gromov-Hausdor sense; 3) the subclasses M of homogeneous manifolds with inner metric and L G of connected Lie groups with leftinvariant Finslerian metric are everywhere dense in (Ω, d_BGH): It is given a metric characterization of Carnot groups with left-invariant sub-Finslerian metric. At the end are described homogeneous manifolds such that any invariant inner metric on any of them is Finslerian.

In this paper, we shall use a method based on the theory of extensions of left-symmetric algebras to classify complete left-invariant affine real structures on solvable non-unimodular three-dimensional Lie groups.

The main purpose of this paper is to study non-commutative ternary Nambu-Poisson algebras and their Homtype version. We provide construction results dealing with tensor product and direct sums of two (non- commutative) ternary (Hom-) Nambu-Poisson algebras. Moreover, we explore twisting principle of (non-commutative) ternary Nambu-Poisson algebras along with algebra morphism that lead to construct (non-commutative) ternary Hom- Nambu-Poisson algebras. Furthermore, we provide examples and a 3-dimensional classification of non-commutative ternary Nambu-Poisson algebras.

During the last years several papers studying conditional functional equations have appeared. They mostly deal with equations satisfied on some restricted domain and many among them concern equations postulated for orthogonal vectors. In this paper, we define the conditional homomorphisms with the predecessor defined by γ (x)=γ (y) with an even mapping γ. Then, using a fixed point theorem, we investigate the stability of the conditional homomorphisms in Lie C* -algebras.

In our previous publications we have introduced a differential calculus on the algebra U(gl(m))based on a new form of the Leibniz rule which differs from that usually employed in Noncommutative Geometry. This differential calculus includes partial derivatives in generators of the algebra U(gl(m))and their differentials. The corresponding differential algebra omega(U(gl(m)))is a deformation of the commutative algebra omega(Sym(gl(m))). A similar claim is valid for the Weyl algebra W(U(gl(m)))generated by the algebra U(gl(m))and the mentioned partial derivatives. In the particular case m=2 we treat the compact form U(u(2))of this algebra as a quantization of the Minkowski space algebra. Below,we consider non-commutative versions of the Klein-Gordon equation and the Schrodinger equation for the hydrogen atom. To this end we define an extension of the algebra U(u(2))by adding to it meromorphic functions in the so-called quantum radius and quantum time. For the quantum Klein-Gordon model we get (under an assumption on momenta)an analog of the plane wave, for the quantum hydrogen atom model we find the first order corrections to the ground state energy and the wave function.

In this work, we studied the behavior and mobility of telecom subscribers into a train for now and predict a future telecom movement subscriber and have a perfect resources data signal of an operator mobile telecom, we used a deterministic and a probabilistic method. the train in our model example travels through a cellular network and passed into four zones (Z1, Z2, Z3 and Z4), each one is characterized by: topography, numbers of the cellular network, types of network (GSM, GPRS, UMTS ...), numbers of subscribers, types of subscribers(staffs, students, workers and others), numbers of operators (Operator 1, Operator 2 and Operator 3). We have studied statistics in deterministic and probabilistic vision of traffic telecom; the model used is approach to vehicular traffic model.

This paper extends the Helgason-Schiffman formula for the H-function on a semisimple Lie group of real rank one to cover a semisimple Lie group G of arbitrary real rank. A set of analytic 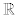-valued cocycles are deduced for certain real rank one subgroups of G. This allows a formula for the c-function on G to be worked out as an integral of a product of their resolutions on the summands in a direct-sum decomposition of the maximal abelian subspace of the Lie algebra g of G. Results about the principal series of representations of the real rank one subgroups are also obtained, among other things.

Given an associative graded algebra equipped with a degree +1 differential Δ we define an A_∞-structure that measures the failure of Δ to be a derivation. This can be seen as a non-commutative analog of generalized BValgebras. In that spirit we introduce a notion of associative order for the operator Δ and prove that it satisfies properties similar to the commutative case. In particular when it has associative order 2 the new product is a strictly associative product of degree +1 and there is compatibility between the products, similar to ordinary BV-algebras. We consider several examples of structures obtained in this way. In particular we obtain an A_∞-structure on the bar complex of an A_∞-algebra that is strictly associative if the original algebra is strictly associative. We also introduce strictly associative degree +1 products for any degree +1 action on a graded algebra. Moreover, an A_∞-structure is constructed on the Hochschild cocomplex of an associative algebra with a non-degenerate inner product by using Connes’ B-operator.

The paper is devoted to structural properties of diassociative algebras. We introduce the notions of nilpotency, solvability of the diassociative algebras and study their properties. The list of all possible nilpotent diassociative algebra structures on four-dimensional complex vector spaces is given.

Let M be an N-dimensional smooth differentiable manifold. Here, we are going to analyze (m>1)-derivations of Lie algebras relative to an involutive distribution on subrings of real smooth functions on M. First, we prove that any (m>1)-derivations of a distribution omega on the ring of real functions on M as well as those of the normalizer of omega are Lie derivatives with respect to one and only one element of this normalizer, if omega doesn’t vanish everywhere. Next,suppose that N= n + q such that n>0, and let S be a system of q mutually commuting vector fields. The Lie algebra of vector fields $\mathfrak{A}_S$ on M which commutes with S , is a distribution over the ring()0MFof constant real functions on the leaves generated by S. We find that m-derivations of $\mathfrak{A}_S$ are local if and only if its derivative ideal coincides with $\mathfrak{A}_S$ itself. Then, we characterize all non local m-derivations of $\mathfrak{A}_S$. We prove that all m-derivations of $\mathfrak{A}_S$ and of the normalizer of $\mathfrak{A}_S$ are derivations. We will make these derivations and those of the centralizer of $\mathfrak{A}_S$ more explicit.