सामान्यीकृत झूठ सिद्धांत और अनुप्रयोगों का जर्नल

The review is devoted to a novel Lie-algebraic approach to studying integrable heavenly type multi-dimensional dynamical systems and its relationships to old and recent investigations of the classical Buhl problem of describing compatible linear vector field equations, its general Pfeiffer and modern Lax-Sato type special solutions. Eespecially we analyze the related Lie-algebra structures and integrability properties of a very interesting class of nonlinear dynamical systems called the dispersionless heavenly type equations, which were initiated by Pleban′ski and later analyzed in a series of articles. The AKS-algebraic and related -structure schemes are used to study the orbits of the corresponding co-adjoint actions, which are intimately related to the classical Lie–Poisson structures on them. It is demonstrated that their compatibility condition coincides with the corresponding heavenly type equations under consideration. It is shown that all these equations originate in this way and can be represented as a Lax compatibility condition for specially constructed loop vector fields on the torus. The infinite hierarchy of conservations laws related to the heavenly equations is described, and its analytical structure connected with the Casimir invariants, is mentioned. In addition, typical examples of such equations, demonstrating in detail their integrability via the scheme devised herein, are presented. The relationship of a very interesting Lagrange–d’Alembert type mechanical interpretation of the devised integrability scheme with the Lax–Sato equations is also discussed.

The aim of this paper is to introduce a new concept for strong almost Pringsheim convergence with respect to an Orlicz function, combining with Riesz mean for triple sequences and a triple lacunary sequence. We also introduce and study statistics convergence of Riesz almost lacunary χ³ sequence spaces and also some inclusion theorems are discussed.

In this work we naturally put forth an open question whether one may construct a scott-topology on transitive binary relational sets (so called TRS). We prove that a TRS gives rise to several natural topologies defined in terms of the given TRS structure. Mainly, we consider directed topologies and scott topologies on TRS and their interactions with the continuity property of TRS. Most of our results are generalizations of corresponding results in references as we will illustrate. Sometimes we need pre-ordered sets instead of TRS.

Contraction is one of the most important concepts that motivated by numerous applications in different fields of physics and mathematics. In this work, the contractions of complex associative algebras are considered. We focus on the variety A₃(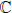) of all complex associative algebras of dimension three (including nonunital). Various contractions criteria are collected and new criteria are proposed to test the possible existence of contraction for each pair of associative algebras. One of the main tools is the use of the low-dimensional cohomology groups of these algebras. As a result, we prove that the variety A₃(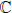) has seven irreducible components, two of dimension 5, four of dimension 7 and one of dimension 9.

In this note we define a notion of Courant pair as a Courant algebra over the Lie algebra of linear derivations on an associative algebra. We study formal deformations of Courant pairs by constructing a cohomology bicomplex with coefficients in a module from the cochain complexes defining Hochschild cohomology and Leibniz cohomology.