Omri F
The purpose of this paper is to give a sufficient condition for the existence and stability of a hybrid limit cycle for the stabilizing control of a class of switched dynamical systems in 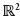 . This is then illustrated on a Induction Heating Appliance.
. This is then illustrated on a Induction Heating Appliance.
Usubamatov R, Abdykerimova D and Dotalieva Z
Kinematics of a rotating object about a fixed axis is well described in science of classical mechanics. All fundamental publications and textbooks contain a mathematical model for an acceleration of a rotating object about a fixed axis that is used for computing of forces acting on an object. Practice of usage for computing an acceleration a rotating object did not show some claims to the known equation. Nevertheless, the detailed analysis of the mathematical model for kinematics of a rotation of an object with acceleration demonstrates its incorrectness. The value of the actual acceleration of the rotating object is less than computed by the known equation. This is reason that running mechanisms are operating without fails because the value of acting forces is bigger than actual one. It means, the component of mechanisms is stronger and heavier than necessary. This paper addresses an acceleration analysis of a rotating object about a fixed axis and presents the mathematical model for computing an acceleration that can be used in engineering.
Haj EA, Khalil H and Hossein M
The elliptic 2-Hessian equation is a fully nonlinear partial differential equation that is related, for example, to intrinsic curvature for three dimensional manifolds. We solve numerically this equation with periodic boundary condition and with Dirichlet boundary condition using a Newton’s algorithm. We verify numerically, by introducing finite difference schemes, the convergence of the algorithm which is obtained in few iterations.
Abdulraheem MZ and Mohammad K
The purpose of this work is to solve Linear Programming (LP) problems using LU factorization. LU method is based on the fact that a square matrix can be factorized into the product of unit lower triangular matrix (L) and upper triangular matrix (U), and the direct solution was obtained without iterations. Three different problem cases were considered and solved using step-by-step calculations as well as using MATLAB. Results show this method is superior than the traditional simplex method with cases of cycling.